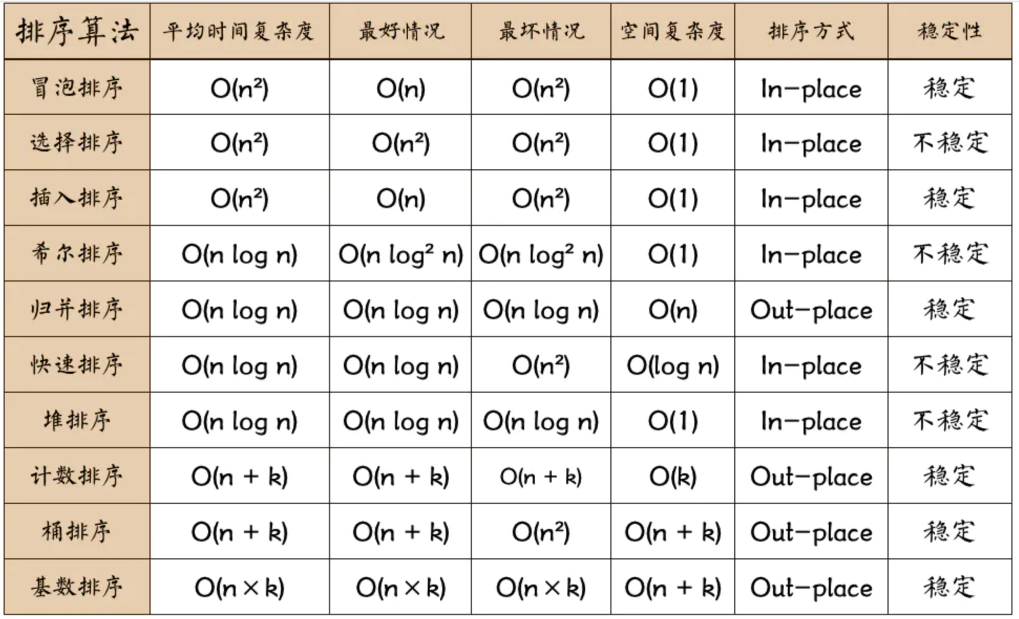
冒泡排序
算法描述
- 比较相邻的元素,如果前一个比后一个大,交换两个元素
- 从最开始的一对到最后一对,这样最后的元素就是数组里最大的数
- 重复以上步骤,除了最后一个
- 重复步骤1-3,知道排序完成。
#python实现
def bubbleSort(nums):
n = len(nums)
if n ==0:
return nums
for i in range(n):
for j in range(n-1-i):
if nums[j]>nums[j+1]:
nums[j],nums[j+1] = nums[j+1],nums[j]
return nums
//Java实现
public static int[] bubbleSort(int[] nums){
n = nums.lengthl
if(n==0){return nums;}
for(int i=0;i<n;i++){
for(int j=0;j<n-1-i;j++){
if(nums[j]>nums[j+1]){
int tmp = nums[j+1];
nums[j+1] = nums[j];
nums[j] = tmp;
}
}
}
}
选择排序
算法描述
从未排序的序列中找到最大(小)元素,放入排序序列的起始位置。再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。
#python 实现
def selectSort(nums):
n = len(nums)
if n==0: return nums
for i in range(n):
minIndex = i
for j in range(i,n):
if nums[j]<nums[minIndex]:
minIndex = j
tmp = nums[minIndex] #最小元素和无序区第一个数交换
nums[minIndex] = nums[i]
nums[i] = tmp
return nums
//java实现
public static int[] selectSort(int[] nums){
n = nums.length;
if(n==0){return nums;}
for(int i=0;i<n;i++){
int minIndex=i;
for(int j=i;j<n;j++){
if(nums[minIndex]<nums[j]){minIndex = j;}
}
int tmp=nums[minIndex];
nums[minIndex] = nums[i];
nums[i] = tmp;
}
return nums;
}
插入排序
算法描述
直接插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
一般来说,直接插入排序都采用in-place(原地算法)在数组上实现。具体算法描述如下:
1)从第一个元素开始,该元素可以认为已经被排序;
2)取出下一个元素,在已经排序的元素序列中从后向前扫描;
3)如果该元素(已排序)大于新元素,将该元素移到下一位置;
4)重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
5)将新元素插入到该位置后;
6)重复步骤2~5。
#python实现
def insertionSort(nums):
n = len(nums)
if n==0: return nums
for i in range(1,n):
cur = nums[i] #取出未排序部分的第一个元素
preIndex = i-1 #排序部分最后一位元素
while(preIndex>=0 and cur<nums[preIndex]): #跟前一位元素对比
nums[preIndex+1] = nums[preIndex]
preIndex-=1 #从后往前比较
nums[preIndex+1] = cur #插入元素
return nums
public static int[] insertionSort(int[] nums ){
int n = nums.length;
if(n==0){return nums;}
int cur;
for(int i=1;i<n;i++){
cur = nums[i];
preIndex = i-1;
while(preIndex>=0 && cur<nums[preIndex]){
nums[preIndex+1]=nums[preIndex];
preIndex--;
}
}
nums[preIndex+1] = cur;
}
时间复杂度
直接插入排序平均时间复杂度为O(n2),最好时间复杂度为O(n),最坏时间复杂度为O(n2)。
最好情况:如果待排序元素本来是正序的,比较和移动元素的次数分别是 (n - 1) 和 0,因此最好情况的时间复杂度为O(n)。
最坏情况:如果待排序元素本来是逆序的,需要进行 (n - 1) 趟排序,所需比较和移动次数分别为 n * (n - 1) / 2和 n * (n - 1) / 2。因此最坏情况下的时间复杂度为O(n2)。
归并排序
算法描述
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
1)把长度为 n 的输入序列分成两个长度为 n / 2 的子序列;
2)对这两个子序列分别采用归并排序;
3)将两个排序好的子序列合并成一个最终的排序序列。
时间复杂度稳定为O(nlogn),空间复杂度O(n),递归引用空间
def mergeSort(nums):
if len(nums)<=1:
return nums
mid = len(nums)/2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
return merge(left,right)
def merge(left,right):
"""合并两个已拍好的列表,产生一个新的已排序好的列表"""
result=[]
i = 0
j = 0
#队列表中的两个元素两两对比
#将最小的元素,放到result中,并对当前下标+1
while i<len(left) and j<len(right):
if left[i]<=right[i]:
result.append(left[i])
i+=1
else:
result.append(right[i])
j+=1
result += left[i:]
result += right[j:]
return result
public static int[] mergeSort(int[] nums){
if(nums.length<=1){
return nums;
}
int mid = nums.length/2;
int[] left = Arrays.copyOfRange(nums,0,mid);
int[] right = Arrays.copyOfRange(nums,mid,nums.length);
return merge(mergeSort(left),mergeSort(right));
}
public static int[] merge(int[] left, int[] right){
int[] result = new int[left.length + right.length];
int i=0,j=0,k=0;
while (i < left.length && j < right.length) {
if (left[i] <= right[j]) {
result[k++] = left[i++];
} else {
result[k++] = right[j++];
}
}
while (i < left.length) {
result[k++] = left[i++];
}
while (j < right.length) {
result[k++] = right[j++];
}
return result;
}
快速排序
算法描述
快速排序使用分治法来把一个数列分为两个子数列。具体算法描述如下:
1)从数列中挑出一个元素,称为 “基准”(pivot);
2)重新排序数列,所有比基准值小的元素放在基准前面,所有比基准值大的元素放在基准的后面(相同的数可以到任一边),该基准就处于数列的中间位置。这称为分区(partition)操作;
3)递归地(recursive)对小于基准值元素的子数列和大于基准值元素的子数列进行快速排序。
def quicksort(nums):
if len(nums)<2:
return nums
else:
cur = nums[0]
less = [i for i in nums[1:] if i<cur]
greater = [i for i in nums[1:] if i>=cur]
return [quicksort(less)+[cur]+quicksort(greater)]
堆排序
算法描述
堆排序是一种树形选择排序方法,它利用了堆这种数据结构。在排序的过程中,将array[0,…,n-1]看成是一颗完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的关系,在当前无序区中选择关键字最大(最小)的元素。
② 概念
堆:堆是一种完全二叉树,且满足所有父节点的值均大于等于(或小于等于)其子节点的值。
大根堆(最大堆):满足所有父节点的值均大于等于其子节点的值的堆称为大根堆,堆顶元素是堆中元素的最大值。
小根堆(最小堆):满足所有父节点的值均小于等于其子节点的值的堆称为小根堆,堆顶元素是堆中元素的最小值。
堆的顺序存储结构:使用顺序数据结构(数组)存储堆,表示方法为:
1.数组按层序遍历的顺序存放完全二叉树的结点,下标为 0 处为堆顶,下标为 len - 1 处为堆尾。
2.结点 i 如果存在左孩子(下标不超过 len - 1 就存在),左孩子的下标为(2 * i + 1);如果存在右孩子,右孩子的下标为(2 * i + 2)。结点 i 的父结点下标为 (i - 1) / 2 (下标为 0 的结点除外,它没有父结点)。最后一个非叶子结点即为堆尾元素的父结点,下标为 (len - 1 - 1) / 2 = (len - 2) / 2。
③ 算法描述
1)将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为(n-1),则整个排序过程完成。
//声明全局变量,用于记录数组array的长度;
static int len;
/**
* 堆排序算法
* @param array
* @return
*/
public static int[] HeapSort(int[] array) {
len = array.length;
if (len == 0) return array;
//1.构建一个大根堆
buildMaxHeap(array);
//2.循环将堆顶(最大值)与堆尾交换,删除堆尾元素,然后重新调整大根堆
while (len > 0) {
swap(array, 0, len - 1);
len--; //原先的堆尾进入有序区,删除堆尾元素
adjustHeap(array, 0); //重新调整大根堆
}
return array;
}
/**
* 自顶向下调整以 i 为根的堆为大根堆
* @param array
* @param i
*/
public static void adjustHeap(int[] array, int i) {
int maxIndex = i;
//如果有左子树,且左子树大于父节点,则将最大指针指向左子树
if (2 * i + 1 < len && array[2 * i + 1] > array[maxIndex])
maxIndex = 2 * i + 1;
//如果有右子树,且右子树大于父节点,则将最大指针指向右子树
if (2 * i + 2 < len && array[2 * i + 2] > array[maxIndex])
maxIndex = 2 * i + 2;
//如果父节点不是最大值,则将父节点与最大值交换,并且递归调整与父节点交换的位置。
if (maxIndex != i) {
swap(array, maxIndex, i);
adjustHeap(array, maxIndex);
}
}
/**
* 自底向上构建初始大根堆
* @param array
*/
public static void buildMaxHeap(int[] array) {
//从最后一个非叶子节点开始自底向上构造大根堆
for (int i = (len - 2) / 2; i >= 0; i--) {
adjustHeap(array, i);
}
}
二分查找(补充)
public statin int binarySearch(int[] arr, int target){
int low = 0;
int high = arr.length -1;
int mid = 0;
if(target<arr[low] || target>arr[high]||low>high){return -1;}
while(low<=high){
mid = low+(high-low)/2; //避免int溢出
if(arr[mid]>target){
high = mid-1; //大于 -1
}
if(arr[mid]<target){ //小于+1
low = mid+1;
}
else{return mid;}
}
return -1;
}

