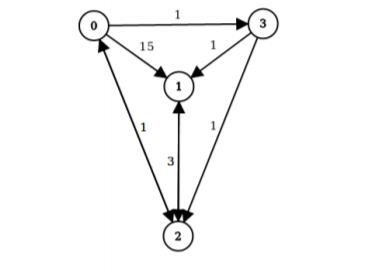
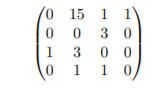该项目的目标是设计并行算法,并使用Dijkstra算法来解决全源最短路径问题(All-Pairs Shortest Paths Problem) 。
全源最短路径问题: 确定给定图中每对顶点之间的最短图形距离。
在全源最短路径问题中,每个顶点到所有顶点的最短距离可以分别计算。因此,MPI框架可用于并行计算最短距离,每个进程负责一部分顶点计算。根据顶点数量和平行比例平均分配所有顶点。在每个进程中,根据当前进程号和进程总数确定每个进程的计算范围。
首先,程序在根进程中读取图形的输入数据,并通过MPI_Bcast函数将图形的顶点数和权重矩阵分配给每个进程。为了方便处理,将图的数据读入并存储在一维数组中。接下来,在每个过程中,使用djkstra算法计算从每个顶点到范围内所有顶点的最短距离。计算完成后,通过MPI_Gatherv函数将每个进程的计算结果收集到根进程中,最后将结果保存到根进程中的文件中。
部分代码
djkstra algorithm 的实现
/**
* Using djkstra algorithm to calculate the shortest distance between vertices
*
* @param graph Graph struct
* @param start start number of the vertex that calculates the shortest distance
* @param end end number of the vertex that calculates the shortest distance
* @return
*/
int *djstra(Graph *graph, int start, int end) {
int n = graph->vertices_number;
int *local_result = (int *) malloc(sizeof(int) * (end - start + 1) * n);
memcpy(local_result, graph->adjacency_matrix + start * n, (end - start + 1) * n * sizeof(int));
int *mark = (int *) malloc(sizeof(int) * n);
int vertex_no = start;
for (; vertex_no <= end; vertex_no++) {
memset(mark, 0, sizeof(int) * n);
int i = 0;
while (i++ < n) {
int offset = (vertex_no - start) * n;
int vertex = get_min(local_result + offset, mark, n);
mark[vertex] = 1;
int j = 0;
for (; j < n; j++) {
if (mark[j] == 1) {
continue;
}
// updating distance
if (local_result[offset + vertex] + graph->adjacency_matrix[vertex * n + j] <local_result[offset + j]) {
local_result[offset + j] = local_result[offset + vertex] + graph->adjacency_matrix[vertex * n + j];
}
}
}
}
return local_result;
}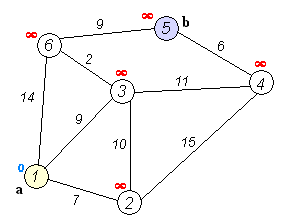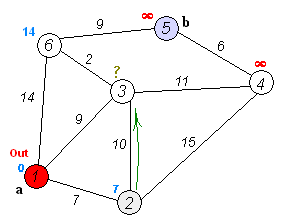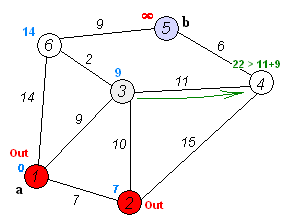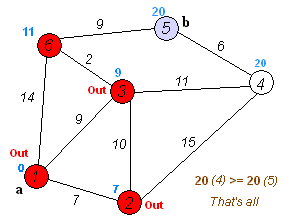
连续迭代,每次找到距离最短的顶点,更新从该顶点到其他顶点的距离,直到找到到所有顶点到起点的最短距离。这是使用Dijkstra 单源最短路径算法,将此函数broadcast到MPI的其他节点,并分配给其相应的图中的顶点并完成此算法,就可以解决全源最短路径问题。
输入文件
输入文件格式本质上是有向加权图的扁平邻接矩阵。所有权重均为正整数。这些是二进制文件,因此需要将其读取。每个文件包含:
- 顶点数 (numV)
- numV x numV 个整数,指定所有连接的权重
例如:
对应如下矩阵:
使用
./run.sh host 文件定义了MPI 所需要的节点数量,最优使用数量在16个左右
输出
./print_bin_result test_data/xxx.out